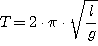
wobei:
l: Länge des Pendel
g: Fallbeschleunigung
Mathematisches Pendel
Das mathematische Pendel stellt eine Idealisierung des Fadenpendels dar: Eine Punktmasse hängt an einem masselosen Faden. Für die Schwingungsdauer T kann folgende Formel verwendet werden:
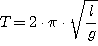
wobei:
l: Länge des Pendel
g: Fallbeschleunigung
Da da mathematische Pendel keine exakte harmonische Schwingung ausführt, hängt die Schwingungsdauer von der Amplitude ab. Zusätzlich muss beim Fadenpendel das Trägheitsmoment der Masse (hier als Kugel mit einer homogenen Masseverteilung angenommen) berücksichtigt werden. Folgende Näherungsformel kann verwendet werden:
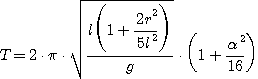
wobei:
: Amplitude im Bogenmass
r: Radius der Kugelmasse
Das Applet berücksichtigt das Trägheitsmoment der Masse nicht.
Der entsprechende Therm der Näherungsformel (Faktor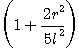 
) wurde daher weggelassen.
Das Applet berechnet die Schwingungsdauer zusätzlich mit Hilfe eine Simulation. Die Schrittweite der Simulation beträgt Delta t. Ein guter Wert für Delta t ist in der Regel 1E-6. Bei zu kleinen Schrittweiten wird die Rechenzeit zu gross. Das Applet akzeptiert Werte die kleiner als T/1E7 nicht.
Schwingungsdauer eines Mathematischen Pendels
Ein mit Delphi erstelltes Windows Programm können Sie hier downloaden. Delphi von Inprise ist übrigens in meinen Augen ein sehr gutes Werkzeug (in der Standardversion zu einem durchaus erschwinglichen Preis).